PGD meets Eigenraum
Eine kleine Wasserstandsmeldung und ein Podcasttipp.
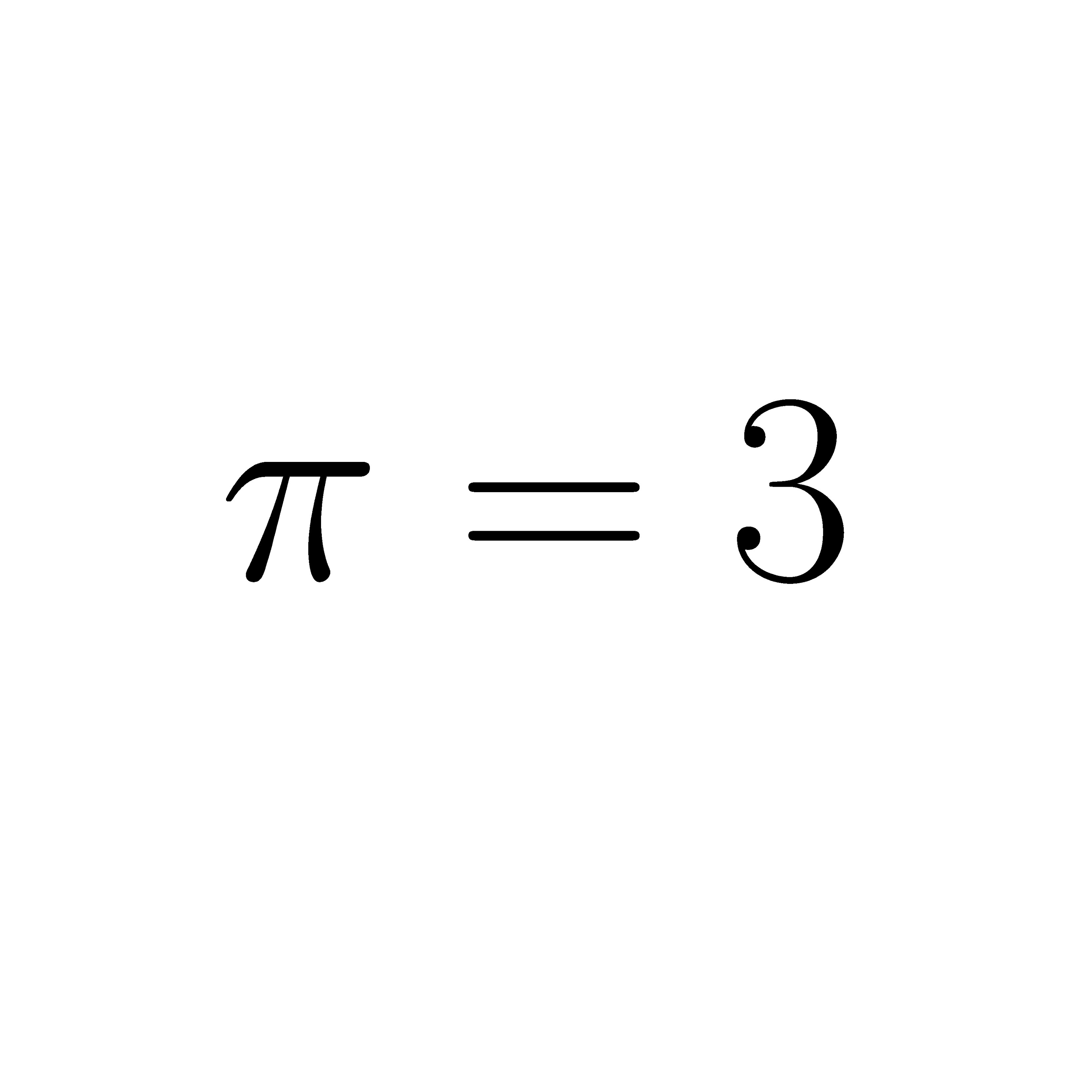
Eine kleine Wasserstandsmeldung und ein Podcasttipp.
Alexander der Große hat den gordischen Knoten einfach zerschlagen. Oder war es ein Unknoten und er hätte das Problem auch stetig lösen können? Wir besprechen, wie man Knoten mathematisch definiert und klassifiziert, was Thomas leider mit einem 3D-Druck Problem gar nicht weiter bringt.
"Es gibt Beweise mit Löchern, Beweise mit Fehlern und Beweise, die nur zwei Leute auf der ganzen Welt verstehen. [...] Um wirklich zu wissen, welche Resultate man glauben kann, muss man Teil eines inneren Zirkels sein und Zugang zu den Experten haben, die den Konsens herstellen." sagt Kevin Buzzard. Oder man beweist die Sätze formal.
Wenn a+b=c gilt, wie verhalten sich die Primfaktoren von a, b und c? Ausgehend von einer "einfachen" Frage der Zahlentheorie, kommen wir über die Suche nach außerirdischem Leben zu Fermats letztem Satz und fake news in der Mathematik.
Ist das noch Kunst oder doch eher Mathematik? Dies ist eine Folge über den wohl bedeutendsten Künstler seit den Malern der Renaissance, der sich mit Mathematik und der Abbildung mathematischer Phänomene beschäftigt hat.
Warum ist 2+2=4 und wie definiert man 2 oder 4? Eine Folge über das Zählen und die Zahlen.
Kann man messen, wie krumm etwas ist? Klar geht das! Sogar, wenn es sich bei dem "etwas" um recht abstrakte mathematische Objekte handelt. Und was hat das alles mit dicken und dünnen Dreiecken, Pferdesätteln, Robotern und Pringels zu tun?
Das Auswahlaxiom ist offensichtlich wahr, der Wohlordnungssatz offensichtlich falsch, und niemand weiß genau, was es mit Zorns Lemma auf sich hat.
Lange war unklar, ob die Pyramidenform wirklich die platzsparendste Möglichkeit ist Orangen zu stapeln. Schon Johannes Kepler war sich sicher, dass das so sein muss. Als Thomas Hales fast 400 Jahre später seine Vermutung bewies verstand kein Mensch den Beweis. Warum er sich trotzdem sicher sein kann alles richtig gemacht zu haben erfahrt ihr in dieser Episode.
Es geht mal wieder in die vierte Dimension und wir erkunden, was es dort für vielfältige, irrationale Polytope gibt. Außerdem: in welcher Dimension verschwinden die Socken?
Nächste Woche startet wieder ein neues Semester und viele Studis werden zum ersten Mal in einer Mathevorlesung sitzen. Wir besprechen, was man unbedingt tun oder nicht tun sollte und welche Fehlvorstellungen es zum Mathematikstudium gibt.
Was ist ein mathematisches Gebiet? Wie entsteht es und warum bekommt es die Nummer 62R01? Eine Fallstudie am Beispiel der algebraischen Statistik. Ach ja, und Krabben!
Wer für die Sommerpause noch ein neues Hobby sucht sollte diese Folge hören. Wir diskutieren die Möglichkeiten und Schwierigkeiten des (mathematischen) Origami und klären warum es so schwierig ist einen Beipackzettel wieder ordentlich in die Packung zurück zu bekommen.
Eine Internetbewegung hält Pi für falsch. Das gilt es zu klären.
1934 treffen sich sechs junge französische Mathematiker im Café Copulade und beschließen die Grundlagen der Mathematik abgeschlossen und stringent neu aufzuschreiben. Sie wollen die Lehrbuchsituation verbessern.
Leben wir in einem Kontinuum oder doch in einer diskreten Simulation? Und warum können die Spaghetti so effizient sortiert werden?
Tetraeder, Oktaeder, Würfel, Dodekaeder und Ikosaeder sind die symmetrischsten Polyeder. Es gibt in drei Dimensionen auch nur diese fünf. Was das ganze mit Erdbeeren, eckenvermeidenden Wanderungen und den Etruskern zu tun hat erfahrt ihr in dieser Episode.
Gibt es wirklichen Zufall, oder erscheint uns nur zufällig, was zu kompliziert für eine Beschreibung ist? Wir sprechen über ein zufälliges Paradoxon, Katzen auf Pluto und andere physikalische Phänomene, Messbarkeit von Zufall und über (un-)echte Zufallszahlen.
Melanie Stefan hat 2010 in Nature dazu aufgerufen, dass WissenschaftlerInnen einen CV des Scheiterns schreiben sollten. Welche Rolle spielt das Scheitern in der Wissenschaft? Warum hat das alltägliche Scheitern keinen Platz im wissenschaftlichen Dialog? Sollten wir mehr über das reden, was nicht klappt?
Wir reden über eine interessante Naturkonstante, den Exponenten der Matrixmultiplikation. Ist er zwei, wäre Matrixmultiplikation genauso schnell möglich wie Matrixaddition. Ist er nicht zwei, was soll er dann sein?
Man hat eine Sache erst richtig verstanden, wenn man ein Bild zeichnen kann. Oder? Es geht im (Über-)vereinfachung. Ums Einfache und Generelle und um die Frage ob, oder wozu wir Bilder brauchen in der Mathematik.
Es geht um die Frage, ob Mathematik jemandem gehören kann, welche Rechte und Pflichten sich aus einem Beweis ergeben, und mal wieder, was Mathematik überhaupt ist.
Der 12. Februar wäre der optimale Tag gewesen diese Episode aufzuzeichnen. Symmetrie kommt aus dem Altgriechischen und bedeutet Ebenmaß. Wie man Symmetrie mathematisch fassen kann - darum geht es hier.
Wie berechnet man eigentlich eine Quadratwurzel? Darum, um Gartenplanung und um Quake 3 Arena geht's in dieser Folge.
Kaffee oder Tee? Ja! Hier auf einen kleinsten gemeinsamen Nenner zu kommen ist die Quadratur des Kreises! Wir sprechen über Mathematik und Logik in der Alltagssprache, darüber wie (Fach-)Begriffe und Redewendungen entstehen und wie sich die Verwendung von Ausdrücken unterscheidet oder beeinflusst.
Im Jahr 1994 findet Thomas Nicely bei der Berechnung der Brunsschen Konstante heraus, dass der Intel Pentium Prozessor den Kehrwert von 824.633.702.441 nicht korrekt (genug) berechnet. Die Ursache ist eine fehlerhafte Tabelle im Design des Pentium Chips.
Wie viele Möglichkeiten es gibt das Haus vom Nikolaus zu zeichnen, wie man erkennt, ob das Doppelhaus mit Weihnachtsmann auch so gezeichnet werden kann und was das ganze mit Brücken in Königsberg zu tun hat erzählen wir euch in dieser Folge.
Von Logarithmentafeln bis Trump geht es diesmal um die Verteilung der ersten Ziffer von Zahlen -- das Benfordsche Gesetz.
Heute verraten wir euch, wie man mit nur 33% der Stimmen trotzdem eine Wahl gewinnt.
Von Krankenhausrobotern über Zopfgruppen zu platonischen Körpern testen wir aus, was Podcast kann und darf.